作者简介:俞明涛(1994—),男,浙江上虞人,硕士研究生,主要从事数值分析及模拟方面的研究。E-mail: 767903027@qq.com
间接地下滴灌是一种能有效减少地表蒸发、提高水分运输效率的新型滴灌方式。虽然土壤水分运动模拟已成为优化滴灌的重要工具,但由于土壤水力特征参数难以确定,模拟结果往往不够精确。为此,基于室内间接地下滴灌实验数据,利用HYDRUS-2D软件对土壤水力特征参数进行反演尝试,并探究边界均匀出水时,不同规格(直径、高度)的间接地下滴灌导水装置下形成的土壤水分分布差异。结果表明,HYDRUS-2D软件能有效地反演土壤水力特征参数,用反演参数模拟的土壤含水量和湿润距离与实测值吻合良好,基于3个反演参数和4个反演参数的模拟效果差异不大,计算模型的纳什效率系数分别为0.716和0.714。灌溉时不同直径、相同透水边界高度的装置对侧边和底部的含水量分布影响不大,而相同直径、不同透水边界高度的装置对侧边和底部的含水量分布影响较大。研究结果可为间接地下灌溉时导水装置规格的选取与农业水分精准管理提供科学依据。
Indirect subsurface drip irrigation is a new drip irrigation method, which can effectively reduce surface evaporation and improve water transport efficiency in soil. Although numerical modeling of soil water movement has become an important tool for optimizing irrigation, the predictions are often not sufficiently accurate due to the uncertainty of soil hydraulic property values. In this study, based on the laboratory data from the experiments on indirect subsurface drip irrigation, it was attempted to infer the soil hydraulic parameters by using HYDRUS-2D software. Also, the difference in soil water content distribution was numerically explored for drip irrigation devices with different specifications (diameter and height). The results showed that the HYDRUS-2D software could effectively infer the soil hydraulic parameters. The simulated soil water content and wetting distance using the inferred soil hydraulic parameters agreed well with the measured values. The differences in simulated results based on the 3 and 4 inferred parameters were not significantly different. The calculated Nash-Sutcliff model performance coefficient was 0.716 and 0.714, respectively. The irrigation device with the same permeable boundary height but different diameter had little effect on soil water content distribution around the water guide device, while the device with the same diameter but different permeable boundary height had a bigger effect on water content distribution. The results obtained in this study could provide a scientific basis for the selection of water guide device specifications and the precision management of agricultural water for indirect subsurface irrigation.
干旱地区常年降水稀少, 蒸发强烈, 水资源缺乏, 如何提高农业水的利用效率是干旱地区农业发展所要解决的首要问题。间接地下滴灌系统由普通地表滴灌系统与布置在滴头下方土壤当中的导水装置构成, 不仅能像地下滴灌那样将灌溉水直接运输到作物根区, 减少地表蒸发, 而且能有效解决地下滴灌滴头孔堵塞的问题, 适合种植密度不大的作物灌溉, 是一种新型节水、高效的灌溉系统[1]。
合理地设计间接地下滴灌系统, 需要知道灌溉过程中导水装置附近含水量的分布情况, 以使根区土壤具有较大的含水量, 同时使通往地表和向下渗漏的水量最小[2]。土壤湿润体的实际形状和土壤含水量具体分布状态受很多因素的影响, 如土壤水力特征参数、土壤初始含水量、边界条件、滴头流量、根分布状态、蒸发和蒸腾条件等[3]。此外, 影响间接地下滴灌中土壤水分分布状态的主要因素还包括导水装置底部直径和侧面透水边界高度[4]。随着土壤科学与计算技术的发展, 基于非饱和土壤水运动理论的数学模型能有效地估算灌溉过程中土壤含水量的变化情况[5]。许多学者用HYDRUS-2D软件对土壤水运动进行了大量的数值模拟, 发现该软件的模拟精度高且应用范围广泛[6, 7, 8, 9, 10]。
土壤水力特征参数是求解土壤水运动方程的关键[11], 目前多采用实验的方法获取[12], 但由于实验样品的边界效应, 测得的土壤水力特征参数往往无法反映田间尺度的实际情况。近些年, 用反演模型推求土壤水力特征参数变得越来越受欢迎[13, 14]。饶元等[15]采用带有自适应差分演化的马尔科夫链蒙特卡洛方法成功地反演了土壤水力特征参数; Nakhaei等[16]基于积水入渗实验测得的观测点土壤含水量与温度数据, 用HYDRUS-2D软件成功反演了土壤水力特征参数和热运移参数; 张吉孝等[17]基于室内沟灌土壤入渗实验测得的观测点含水量数据, 用HYDRUS-2D和RETC软件进行数值模型, 分别求得土壤水力特征参数, 发现用HYDRUS-2D软件反演的结果更加准确可靠。在间接地下滴灌过程中不同规格的导水装置对土壤水分分布影响的研究方面, 赵伟霞等[18]用恒定水头钻孔积水入渗法求解了土壤饱和导水率的稳态模型, 对间接地下滴灌导水装置参数与滴头流量间的关系进行了探讨。但关于不同直径或不同透水边界高度的导水装置下土壤水分分布的模拟报道在本研究检索范围内仍相当有限。
本研究的主要目标主要有3个:(1)利用土壤含水量实测数据和HYDRUS-2D软件反演土壤水力特征参数, 并比较不同反演变量数对结果的影响; (2)用不同工况的土壤湿润峰距离的实测数据独立验证反演参数的可靠性; (3)探究间接地下滴灌时导水装置不同直径和不同透水边界高度对土壤含水量分布的影响, 为提高土壤水运动模拟精度与指导间接地下滴灌设计时选择合适的导水装置规格提供科学依据。
1.1.1 土壤水分运动基本方程
在轴对称的条件下, 可将土壤入渗简化成径向和垂直2个方向, 若不考虑根系吸水情况, 并假设土壤均质且各向同性, 则描述土壤水流运动的Richards方程[19]可表述为
式中:θ 为土壤体积含水率, D
1.1.2 土壤水力特征函数方程
土壤水力函数选择van Genuchten-Mualem公式[20], 其表达形式为
K
θ e=
式中:Ks为土壤饱和导水率, θ e为土壤相对饱和度, θ r为土壤剩余体积含水率, θ s为土壤饱和体积含水率, h表示土壤水压力, α 和n是与土壤物理性质有关的经验拟合参数(或曲线性状参数), m=1-1/n。
1.1.3 HYDRUS-2D软件的反演参数原理
HYDRUS-2D软件通过优化土壤水力特征参数, 使得选取的观测值与模拟值之间的误差最小化。具体地:HYDRUS-2D软件采用Marquardt-Levenberg优化算法使目标函数最小化, 该优化算法同时具有牛顿法和梯度法的优点, 收敛较快。有关使用HYDRUS-2D软件进行参数反演的详细介绍可见文献[4]。
1.1.4 模型评估标准
本文采用纳什效率系数(NSE)[21]、均方根误差(RMSE)和绝对平均误差(MAE)作为模型的评价指标。
本文采用的实验数据来自文献[22, 23]。实验的情况简述如下, 详细描述可见文献[22, 23]。实验装置为一个0.5 m× 0.5 m× 0.5 m的立方体透明玻璃土槽。实验时首先将直径为50 mm、长20 cm的PVC管从中间切开, 取一半固定贴在土槽其中一面的中间, 上边缘与土槽齐平, 接着向土槽里加实验土样至距离土槽上边缘15 cm处, 然后向PVC管里加入粒径2~3 mm的砂石, 再将PVC管提升, 以形成5 mm高的透水边界。实验土样容重为1.4 g· cm-3, 土壤颗粒级配情况为:黏粒占5.3%, 粉粒占58.9%, 砂粒占35.8%。在灌水的前1 h内, 每隔5 min记录湿润锋位置, 1 h后每隔10 min记录1次湿润锋的位置, 直至灌水结束。灌水结束后, 立即使用直径1 cm土钻在PVC管外侧直径线上每隔5 cm打一个洞, 共打3个洞, 取土层下40 cm的土样, 每隔5 cm取一次样, 共取土样24个(测点布置见图1), 土样采用烘干法测含水率。
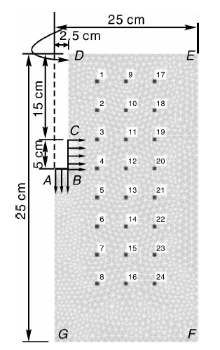 | 图1 有限元计算网格及边界示意图 ■代表土壤含水量测量点。Fig.1 Diagram of finite element mesh with boundary conditions ■ denoted points for measuring soil water content. |
文献[22]报道了2种滴头流量下间接地下滴灌土壤的水盐运移情况, 实验采用的导水装置直径与透水边界高度均为5 cm, 滴头流量分别为2 L· h-1与4 L· h-1, 灌溉结束后在24个测点实测了土壤质量含水率。由于4 L· h-1滴头流量条件下导水装置有较多积水, 故本文选用滴头流量为2 L· h-1时测得的24个测点含水量数据[22]作为研究对象。通过对土壤质量含水率的转化, 24个测点的土壤体积含水率见表1。
| 表1 各观测点体积含水率值 Table 1 Volumetric soil water content for each observation point |
文献[23]报道了不同滴头流量对土壤湿润体特征的影响, 实验采用的导水装置直径与透水边界高度均为5 cm, 滴头流量分别为1.5、2、3、4 L· h-1。基于实验过程中量测的土壤湿润距离, 拟合不同滴头流速时水平和垂直湿润距离与时间的方程。本文根据文献[23]的拟合方程, 分别计算了实验过程中滴头流量为1.5、3、4 L· h-1时的土壤湿润距离(表2)。
| 表2 实验过程中不同时间的土壤湿润距离 Table 2 Measured time and wetting distance during experiments |
针对上述实验数据, 本文确定以下2种工况, 即反演工况和验证工况。反演工况:用实验滴头流量为2 L· h-1时测得的土壤含水量(表1)作为反演数据推求土壤水力特征参数; 验证工况:用滴头流量分别为1.5、3、4 L· h-1时测得的土壤湿润距离数据(表2)对反演的土壤水力特征参数的可靠性进行验证。
HYDRUS-2D软件带有基于神经网络的传递函数法, 能根据土壤颗粒级配情况预测土壤水力特征参数(Rosetta模型)。作为对比, 本文采用Rosetta模型计算实验土的土壤水力特征参数(表3)。
| 表3 土壤水力特性参数值 Table 3 Soil hydraulic parameter values |
如前所述, 本文基于HYDRUS-2D软件并结合表1的观测数据推求了土壤水力特征参数。第一组数值实验是以Rosetta法得出的土壤水力特征参数值作为反演参数的初始值, 对θ s、α 、n和Ks进行反演, 4个反演参数的搜索区间分别设为0.35~0.6、0.01~0.2、1.2~3.0、0.01~0.5。鉴于有文献报道反演参数越少或选取观测值种类越多, 反演参数结果更准确[26], 考虑到土壤饱和含水量的值相对确定, 故第二组数值试验将θ s和θ r取为定值, 即选取Rosetta法得到的值, 对另外3个参数进行反演优化, 优化区间和第一组一样。两组数据实验反演得到的参数见表3。
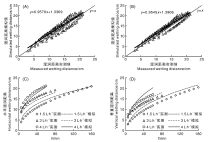
图2是反演工况中的模拟含水量值与实测值的对比, 直观地看出, 3参数的回归拟合线的斜率(0.741 4)比4参数的回归拟合线的斜率(0.730 4)更接近于1。从模型评估结果(表4)看, 用3参数计算的NSE也略好于4参数, 这一结果与已有的文献报道相符[27]。MAE与RMSE这2个指标也反映了同一情况, 即3参数反演的结果略好于4参数, 但总体相差不多。
 | 图2 用3个(A)和4个(B)反演参数获得的土壤含水量模拟值与实测值比较Fig.2 Comparison between simulated and measured values of soil water content obtained from three (A) and four (B) inferred parameters |
| 表4 反演模拟结果统计分析 Table 4 Statistical analysis of simulated results for inference case |
将反演得到的参数对验证工况进行数值模拟, 并对模拟的土壤湿润距离数据与实测值进行比对验证。图3-A、B显示了验证工况中基于3参数和4参数反演的模拟湿润距离与观测值的关系, 表5为验证工况模拟结果的统计分析数据。不难发现:无论是3参数还是4参数反演, 计算的NSE均在0.8以上, 说明模拟值与实测结果吻合良好, 其中基于4参数反演参数计算的湿润距离略接近于实测值。图3-C、D展示了4参数反演时不同流量下的湿润距离与时间变化的模拟值与实测值, 其中, 1.5、3 L· h-1工况的NSE值均在0.75以上, 说明模型预测结果可靠。4 L· h-1工况下垂直湿润距离的NSE为0.546, 可靠度相对较低, 但结果还是可以接受的。总体来说, 3参数与4参数反演得到的土壤水力特征参数均具有较高可靠度, 模拟的土壤湿润距离与实测值较一致。
| 表5 验证模拟结果的统计分析 Table 5 Statistical analysis of simulated results for validation case |
2.3.1 不同直径的导水装置灌溉模拟分析
灌溉滴头流量选用2 L· h-1, 侧边透水边界高度选用5 cm, 选取导水装置直径分别为50、90、130 mm, 总灌溉时长为120 min。
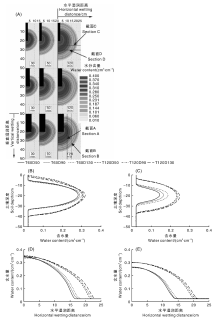
图4展示了不同直径导水装置不同时刻的土壤水分分布状态。可以看出, 间接地下滴灌时土壤湿润体的形状近似于椭圆体, 随着灌溉时间增加, 湿润体范围越来越大。同时可以看出, 随着灌溉装置直径的增大, 湿润距离略有增大, 向上湿润距离降低较为明显, 而向下湿润距离几乎不变, 说明在一定的滴头流量下, 一定程度的增大导水装置直径能减少水分向地表的运移距离。截面B(距导水装置15 cm)比截面A(距导水装置10 cm)的总体含水量低, 灌溉初期截面A处各个直径的最大含水量均在地下18.5 cm的位置, 直径为130 mm(简记为D130)的最大含水量比直径为90 cm(简记为D90)的最大含水量要大9.3%, 比直径为50 cm(简记为D50)的最大含水量大15.9%, 在截面B处这一差距更为明显。不同截面处的最大含水量的差异均随时间的增加而减小, 剖面A处由30 min时的9.3%(D130与D90对比)和15.9%(D130与D50对比)分别降至灌溉结束时的2.5%和4.4%。对剖面C(距灌溉装置底部5 cm)处与剖面D(距灌溉装置底部10 cm)的含水量进行分析发现, 在导水装置底部, 不同直径之间模拟的土壤含水量几乎没有差异, 但随着离导水装置距离的增加, 土壤含水量的差异开始显现, 直径越大, 湿润体周边的含水量相对越小。导水装置直径的增加能增加地面下18.5 cm位置处的含水量, 但对其他位置影响不大。总的来说, 导水装置直径的变化对于侧面和底部的土壤水分分布影响较小。
2.3.2 不同透水边界高度的导水装置灌溉模拟分析
与2.3.1节设置的参数类似, 灌溉滴头流量选用2 L· h-1, 导水装置直径选用50 mm, 选取透水边界高度分别为1、5、10 cm, 总灌溉时长为120 min。
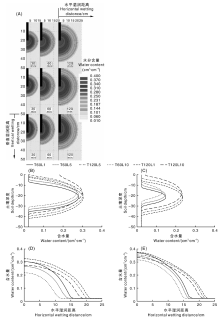
图5为灌溉过程中30、60、120 min时的土壤水分分布。土壤湿润体均近似于椭圆体, 不同的是, 不同透水边界高度的湿润体椭圆轴中心位置不一, 透水边界高度越大, 椭圆轴中心越向上偏移, 而且随着透水边界高度的增大, 灌溉后期土壤表面土体湿润面积会越大, 向下湿润距离则相对减少。灌溉初期, 剖面A处的土壤最大含水量随着侧边透水边界高度的增加而向上移动, 透水边界高度为1、5、10 cm对应的最大含水量的位置分别为地下21.6、18.8、16.4 cm。剖面B处的情况与之类似。从剖面C的水分分布看, 随着透水边界高度的增加, 同一剖面处的含水量逐渐降低, 初始30 min, 透水边界高为10 cm时的含水量比透水边界高为5 cm时整体低0.034 cm3· cm-3, 并比透水边界高为1 cm时整体低0.072 cm3· cm-3, 至灌溉结束, 这一差异分别降至0.021、0.041 cm3· cm-3。剖面D处, 也存在同样的差异, 且初始阶段该差异更大。总体说来, 导水装置透水边界高度的变化对于导水装置侧部和底部都有较大影响, 一定程度的增大导水装置侧边透水边界高度能增加侧面土体含水量, 而底部土体含水量降低。因此, 对于固定直径的导水装置, 透水边界高度的选取应根据其具体情况而定, 过高的透水边界会使得水分移向土表, 造成蒸发损失。
本研究表明, 用HYDRUS-2D软件对土壤水力特征参数进行反演具有较高的可靠度, 基于反演参数模拟的土壤含水量和湿润距离与实测值吻合良好, 3个参数反演的模拟结果与4个参数反演的相差不大, 计算的模型纳什效率系数均达0.71以上。间接地下滴灌过程中, 相同侧边透水高度条件下不同直径的导水装置对于装置周边的土壤含水量影响不大。相同直径不同侧边透水边界高度的导水装置对于装置周边的土壤含水量影响较大, 随着透水边界高度的增加, 导水装置侧面土体的含水量整体上移, 且显著减少导水装置下部土体的含水量, 过大的边界高度会使土体表面湿润面积增大, 造成土壤蒸发水分损失。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|
| [22] |
|
| [23] |
|
| [24] |
|
| [25] |
|
| [26] |
|
| [27] |
|